Kinetic Monte Carlo method development

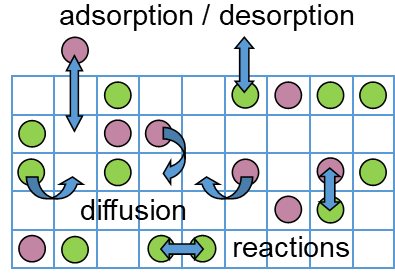
The kinetic Monte Carlo (KMC) method is a simulation technique that allows to achieve a numerical solution to the time evolution of a system that can be described with a Markovian Master equation. That is, the system can exist in a given number of discrete states and can switch between these states according to known transition rates that only depend on the present state of the system. Common applications of the KMC method are diffusion in materials, microkinetic models in catalysis or the growth of crystals or adlayers on surfaces. In heterogeneous catalysis the inputs required for the simulation are the possible processes in the system such as adsorption and desorption of chemicals on the surface, surface diffusion and reactions occurring on the surface as well as their associated transition rates (known as rate constants in catalysis). For given operation conditions at the surface (reactant partial pressures and temperature) not only the catalytic activity, but also other important information such as surface composition, the occurrence of individual reaction steps in the network, or mechanistic aspects like the presence of a dominant reaction mechanism and rate-determining steps therein can be determined. Compared to traditional microkinetic models in catalysis, which often rely on a mean-field approximation (MFA) and consider only average surface coverages, the KMC method fully accounts for correlations, fluctuations and the detailed spatial distributions of the adsorbates at the catalyst surface. Detailed lateral interactions between the adsorbates can also be taken into account using cluster expansion methods. KMC models can potentially achieve a higher accuracy than MFA-based methods, however, the higher accuracy comes at a higher computational cost. This can be especially challenging for surface reactions on metals due to a large disparity in the time scales of different processes, ranging from very fast surface diffusion processes to very slow surface reactions. In order to overcome these issues, we test and develop algorithms for the acceleration of KMC simulations in our in-house KMC code “kmos”. In addition, we work on combing such algorithms with cluster expansion models for lateral interactions.