Repetitive Structures
Design and construction of curved support structures with repetitive parameters
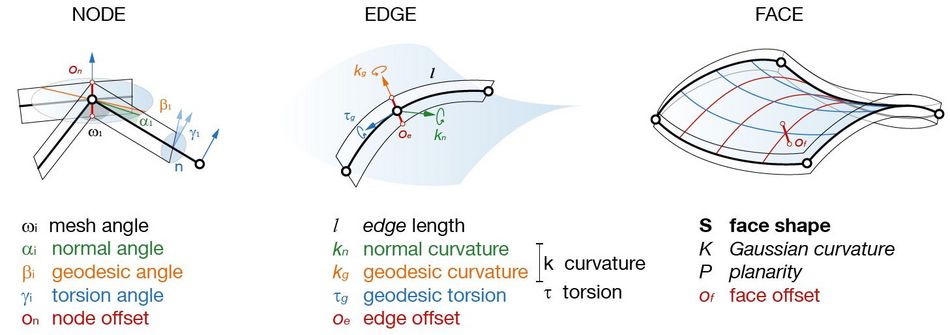
The thesis investigates doubly curved grid structures with the goal to simplify their fabrication. For this purpose, we examine networks with constant geometric parameters, and describe their potentials for design and construction.
A holistic theory of “repetitive structures” is established, which takes into account both geometric and constructive criteria. This allows us to investigate individual parameters in order to create identical building parts. The theory is used to uncover principles of form and structure, and develop a novel method to design and construct elastically formed gridshells.
The work combines theories from differential geometry with knowledge from architecture and structural engineering and thus gains new insights for modern shell design.
Based on a review of scientific publications and built examples, a theoretical framework is created to analyse and design repetitive structures. First, we apply this theory to existing structures, and generate an overview of current and future possibilities of parameter repetition. In a next step, the interdependence between surface, network and parameters are investigated within inductive studies. Through the prototypical design and fabrication of experimental structures, we examine the elastic deformation of building parts as a constructive strategy to achieve repetition.
In a deductive study, the parameters of curvature are related to the deformation behaviour of individual beams. Based on this dependency, a design method is developed, which utilizes the properties of asymptotic curves on a minimal surface. This method provides the geometric condition to construct a doubly curved grid from exclusively straight lamellas and orthogonal nodes. Finally, the method is implemented in an architectural case study: The practical challenges and advantages of repetitive structures are examined through the planning, construction process, and load-bearing behaviour of the “Asymptotic Gridshell”.
Link: Research Pavillion
Doctoral Thesis
Chair of Structural Design
Eike Schling
Assessors: Prof.-Dr.-Ing. Rainer Barthel and Prof. Helmut Pottmann
Looking up at the Asymptotic Gridshell at the TUM. The gridshell was designed along asymptotic curves on a minimal surface. This enables a simplified fabrication from straight and flat lamellas and orthogonal joints.
Overview of the geometric parameters of a curved network. Both discrete and smooth curves are considered.
Systematic investigation of discrete quadrilateral networks on predefined surfaces, depending on certain parameter constraints, like repetitive faces, repetitive edges or repetitive nodes. The blue networks indicate solutions which fulfill all requirements with a fair network.
The theoretical insights were successfully verified within a research pavilion, the Asymptotic Gridshell.
INSIDE\OUT
Designing doubly curved structures with asymptotic curve networks
Planungsteam:
Dipl.-Ing. Architekt Eike Schling
Denis Hitrec
M.Sc. Jonas Schikore
Prof. Dr.-Ing. Rainer Barthel
Lehrstuhl für Tragwerksplanung
Fakultät für Architektur
Technische Universität München
In Kooperation mit:
Brandl, Eitensheim
Aufbau:
Technisches Zentrum:
Matthias Müller, Schlossermeister
Andrea Schmidt
Viktor Späth
Miquel Lloret Garcia
Maximilian Gemsjäger
Rongguang Na
Jakob Wallner
Joram Tutsch
Hannes Pelz
... und viele mehr
Mit Unterstützung von:
Technische Universität Wien, Applied Geometry, Helmut Pottmann
Lehrstuhl für Statik, TUM
Pfeifer Seil- und Hebetechnik, Memmingen
Evolute, Wien
Förderung:
Dr.-Ing. Leonhard-Lorenz-Stiftung
Werner Konrad Marschall und Dr.-Ing Horst Karl Marschall Stiftung
Research Lab
Dekanat der Fakultät für Architektur
During the summer semester 2016 we have investigated the use of these specific curve networks to design gridshells. We have found the most potential in the use of asymptotic curve networks in combination with minimal surfaces. This construction method allows for both straight strips and orthogonal nodes. In the coming year, it is our aim to focus our investigations on the aspects of shape, structure and statics of these networks. After a morphological analysis of minimal surface, we will investigate alternative computational techniques of generating asymptotic line networks. A separate study will look at possible cladding options, with transparent elastic sheet material. To analyse the load bearing behavior of such curve networks, a digital model will be constructed and simulated in FEM. Finally we will verify the use of metal sheets for the construction in real scale, by conducting prototypical tests. Our goal is to publish this research in journals and proceedings and construct a 1:1 research pavilion by October 2017 to be exhibited at the Structural Membranes Conference 2017.