Magnetisierung in GaAs-AlGaAs-Nanostrukturen

Lichtmikroskopische Aufnahme eines mikromechanischen Cantilever-Magnetometers (MCM), aufgeklebt auf ein Saphir-Substrat. Seine Größe beträgt etwa 2x3 mm?. Der sensitive Teil (oben) schwebt über einer Gold-Elektrode, ist lediglich 5.5 µm dick und enthält das niedrigdimensionale Elektronensystem.

Die Gleichgewichts-Magnetisierung ist eine thermodynamische Größe und spiegelt bei der Temperatur T = 0 K den Verlauf der Grundzustandsenergie im Magnetfeld wider. Die Magnetisierung ist deshalb besonders interessant, um etwas über den Einfluss der Vielteilchen-Wechselwirkung auf den Grundzustand eines Elektronensystems zu lernen. Wir verwenden die Magnetisierung im Speziellen, um die Elektron-Elektron-Wechselwirkung (direkte Coulomb-Wechselwirkung, Austausch-Wechselwirkung, Korrelation) in niedrig-dimensionalen Elektronensystemen zu studieren.

Die damit verbundenen magnetischen Signale sind extrem klein. Kommerzielle Magnetisierungsmesssysteme sind generell nicht in der Lage, die Signale zu erfassen. Wir haben deshalb in unserer Forschungsgruppe Messverfahren entwickelt, die uns in die Lage versetzen, die Messgröße mit hoher Präzision zu erfassen. Dies ist insbesondere die Cantilever-Magnetometrie (MCM), bei der wir ein mikromechanisches Prinzip verwenden. Die magnetfeld-induzierte Verbiegung des Cantilevers lesen wir kapazitiv (Kapazitätsmagnetometer) oder interferometrisch aus (faser-optisches Magnetometer).

De Haas-van Alphen-Effekt von niedrigdimensionalen Elektronensystemen

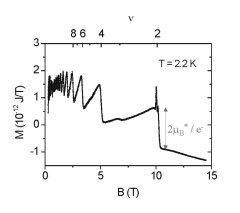
De Haas-van Alphen-Effekt gemessen mit einem MCM an einem 1 mm2 großen 2DES. Dem sägezahn-förmigen Verlauf ist bei Füllfaktor n=2 ein im 2DES induzierter Wirbelstrom überlagert.

Niedrigdimensionale Elektronensysteme stellen wir mit Hilfe moderner Nanostrukturierungsverfahren als Quantendraht- und Quantenpunkt-Strukturen her, die als Modellsysteme für ein-dimensionale bzw. null-dimensionale Elektronensysteme angesehen werden können. Die Strukturen basieren dabei zumeist auf modulationsdotierten GaAs-AlGaAs-Heterostrukturen, die mittels Molekularstrahl-Epitaxie hergestellt wurden. Ziel ist z.B. die Untersuchung von Quantenpunkten, die nur noch wenige Elektronen enthalten und somit als quasi-atomare Systeme ("künstliche Atome") angesehen werden können. Besonders interessant ist hier der Einfluss von Drehimpuls-Umlagerungen im Magnetfeld auf das magnetische Moment. Weiterhin interessiert uns der de Haas-van Alphen-Effekt im zwei-dimensionalen Elektronensystem - besonders im Bereich des ganzzahligen und gebrochenzahligen Quanten-Hall-Effekts. Cantilever-Magnetometer werden auch eingesetzt, um geringste Mengen (µg) neuartig synthetisierter Stoffe magnetisch zu untersuchen.

Siehe hierzu z.B.:

M.A. Wilde, J.I. Springborn, Ch. Heyn, D. Heitmann, and D. Grundler: „Magnetization of GaAs quantum wires with quasi-one-dimensionalelectron systems”, Physica E 22, 729 (2004) [abstract: click here]
M.P. Schwarz, D. Grundler, Ch. Heyn, D. Heitmann, D. Reuter, and A.D. Wieck, „Induced non-equilibrium currents in the magnetization of mesoscopic dots in the quantum Hall regime”, Phys. Rev. B 68, 245315 (2003). [abstract: click here]
M.P. Schwarz, M.A. Wilde, S. Groth, D. Grundler, Ch. Heyn, and D. Heitmann, „Sawtooth-like de Haas-van Alphen oscillations of a two-dimensional electron system ”, Phys. Rev. B 65, 245315 (2002). [abstract: click here]
M.P. Schwarz, D. Grundler, M. Wilde, Ch. Heyn, and D. Heitmann, „Magnetization of semiconductor quantum dots”, J. Appl. Phys. 91, 6875 (2002). [abstract: click here]
M.P. Schwarz, D. Grundler, I. Meinel, Ch. Heyn, and D. Heitmann, „Micromechanical cantilever magnetometer with integrated two-dimensional electron system”, Appl. Phys. Lett. 76, 3564 (2000). [abstract: click here]
I. Meinel, T.M. Hengstmann, D. Grundler, D. Heitmann, W. Wegscheider, and M. Bichler, „Magnetization of the fractional quantum Hall states”, Phys. Rev. Lett. 82, 819 (1999). [abstract: click here]
Dirk Grundler (invited), „Magnetization phenomena in the quantum Hall effect regime”, Festkörperprobleme, Advances in Solid State Physics 39, 221 (1999).