The NEPOMUC remoderator

The brightness is defined as the ratio of the beam intensity and the phase space volume (PSV) occupied by the beam. In general, the PSV consists of three space dimensions and the three conjugated momenta. For continuous, rotationally symmetric beams only the transversal part of the PSV is relevant, which can be simplified to one space dimension — the beam radius — and the conjugated momentum p_r. Consequently, a high brightness accords to a high intensity, a small diameter and a low divergence. For pulsed beams, a sharp beam energy and short pulses become also important (longitudinal part of the PSV).

A small transversal PSV is necessary to attain a small spot at the specimen by focusing with electro- or magnetostatic lenses. This is not only relevant at instruments which are built to achieve an especially high lateral resolution. At instruments where the minimal distance from the last optical element to the sample is limited, a large transversal PSV can restrict the minimal size of the investigated samples. However, the longitudinal energy has to be sufficiently sharp as well due to the limitation of the resolution by chromatic aberration. The longitudinal part of the PSV is always important, if short pulses should be attained with the bunching technique (PLEPS, SPM).

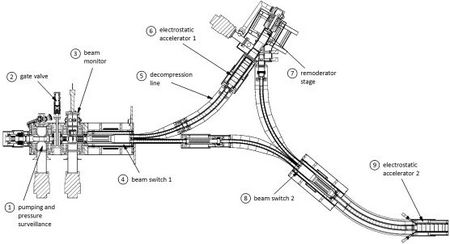
Liouville’s theorem states that the size of the PSV keeps constant under the influence of conservative forces. Therefore, the positron source should be kept as small as possible at the expense of positron yield in order to ensure a proper beam transport without perturbing the PSV [Ref NJP]. Otherwise a reduction of the PSV is only possible by using non-conservative forces. A common method, e.g. in electron microscopes, is to tailor the PSV to a small central region by apertures and collimators (see Fig. 1), since it is easy to produce electron intensities many orders of magnitudes higher than the available positron intensity (even at NEPOMUC). For positron beams the remoderation technique offers a possibility to enhance the beam brightness with much lower intensity losses.

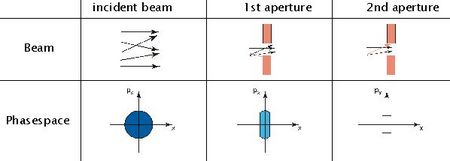
Moderation is the cooling of an ensemble of particles by inelastic scattering processes until it becomes in thermal equilibrium with the surrounding medium. After thermalization the positron can diffuse as a quasi-free particle within the solid. Despite the limited positron lifetime in matter, there is a certain probability that thermalized positrons reach the sample surface before annihilation. Since some materials (e.g. W or Pt) possess a negative positron work function of a few electronvolts these positrons may be emitted into the vacuum with a sharp energy.

For remoderation a positron beam is focused onto a solid with a negative work function. Hence, the beam diameter and the momentum is enlarged so that the PSV keeps constant shrinks according to Liouville’s theorem. Inside the solid the positrons are moderated, i.e. they lose also the transversal momentum induced by the focusing. The reemitted positrons can be extracted in order to generate a narrow beam with low energy spread and a small angular divergence (see figure 2).

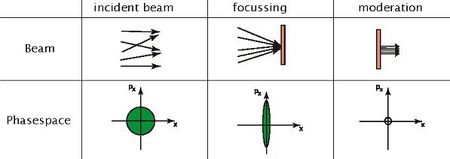
At NEPOMUC the remoderation was implemented in reflection geometry. Hence the primary beam and the remoderated beam passing the same area in opposed direction until they are separated by a magnetic dipole field. In contrast to the transmission geometry thicker and hene more robust crystals can be used. In order to enhance the positron diffusion length and hence the remoderation efficiency a W(110) single crystal is used which can be annealed and surface cleaned in-situ by current heating.

The implemented two positron beam switches enable to guide the primary beam via the remoderator with higher brightness or directly with higher intensity to the experiments (see figure 3).